Quick Sort
➤Quick sort is a sorting algorithm that uses a divide-and-conquer approach. It picks a pivot element and partitions the array into two subarrays, one with elements smaller than the pivot and one with elements larger. This process is repeated recursively until the entire array is sorted. It has an average time complexity of O(n log n).
How Quick-sort works?
1.Select a pivot element, usually the last element in the array.
2.Partition the array into two subarrays, one with elements smaller than the pivot and one with elements larger.
3.Recursively repeat step 2 for each subarray until the subarrays are of length 1 or 0.t
4.Combine the sorted subarrays in the correct order to obtain the sorted array.
Here is an example of how Quick sort would work on the array [7, 2, 1, 6, 8, 5, 3, 4]:
1.Select pivot element: 4
2.Partition into subarrays: [2, 1, 3], [6, 8, 5, 7]
3.Recursively repeat for each subarray:
•[2, 1, 3]: Select pivot element: 3, Partition into subarrays: [2, 1], [3]
•[6, 8, 5, 7]: Select pivot element: 7, Partition into subarrays: [6, 5], [8, 7]
•Repeat for each subarray until subarrays of length 1 or 0 are obtained.
4.Combine sorted subarrays in correct order: [1, 2, 3, 4, 5, 6, 7, 8]
.gif)
How the element compare?
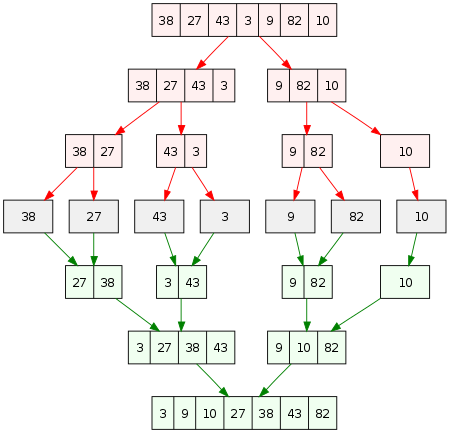
Demonstration of Merge Sort
Optimized Bubble sort Algorithm
1.Insertion Sort for Small Subarrays:
Instead of recursively dividing the array until each subarray
contains only one element, the algorithm switches to Insertion Sort when the subarray size becomes small
(e.g., below a certain threshold). This reduces the overhead of recursive calls and performs better on smaller
or partially sorted subarrays.
2.Skipping Unnecessary Merging:
During the merging process, the algorithm checks if the last element of the left
subarray is already smaller than or equal to the first element of the right subarray. If true, it means the subarrays are already
sorted, and the merging step can be skipped. This optimization reduces unnecessary comparisons and improves performance.
3.Reuse of Auxiliary Array:
Instead of creating a new temporary array for each merge operation, the algorithm allocates
a single auxiliary array at the beginning and reuses it throughout the sorting process. This eliminates the overhead of repeated memory
allocation and deallocation, making the algorithm more efficient.
4.Bottom-Up Merge Sort:
The algorithm can be implemented iteratively using a bottom-up approach. It starts with subarrays
of size 1 and merges them to form larger sorted subarrays. This eliminates the need for recursive calls and can be more cache-friendly,
as it works on adjacent elements. This approach further improves performance.
2.Partition into subarrays: [2, 1, 3], [6, 8, 5, 7]
3.Recursively repeat for each subarray:
•[2, 1, 3]: Select pivot element: 3, Partition into subarrays: [2, 1], [3]
•[6, 8, 5, 7]: Select pivot element: 7, Partition into subarrays: [6, 5], [8, 7]
•Repeat for each subarray until subarrays of length 1 or 0 are obtained.
4.Combine sorted subarrays in correct order: [1, 2, 3, 4, 5, 6, 7, 8]
| Algorithm | Time complexity |
|---|---|
| Best Case | O(n(logn)) |
| Average Case | O(n(logn)) |
| Worst Case | O(n(logn)) |